JavaScript Number精度

约 4229 字大约 14 分钟

2025-01-09

介绍

JavaScript中Number数据的存储遵循 IEEE 754 规范：

先把Number转成二进制科学计数法表示。
然后用64位存储二进制科学计算法的相关参数。

`IEEE_754`介绍

IEEE二进制浮点数算术标准IEEE 754是20世纪80年代以来最广泛使用的浮点数运算标准，为许多CPU与浮点运算器所采用。

这个标准定义了表示浮点数的格式（包括负零-0）与反常值（denormal number），一些特殊数值（（无穷（Inf）与非数值（NaN）），以及这些数值的“浮点数运算符”。它也指明了四种数值舍入规则和五种例外状况（包括例外发生的时机与处理方式）。

IEEE 754规定了四种表示浮点数值的方式：单精确度（32位）、双精确度（64位）、延伸单精确度（43比特以上，很少使用）与延伸双精确度（79比特以上，通常以80位实现）。只有32位模式有强制要求，其他都是选择性的。

大部分编程语言都提供了IEEE浮点数格式与算术，但有些将其列为非必需的。例如，IEEE 754问世之前就有的C语言，现在包括了IEEE算术，但不算作强制要求（C语言的float通常是指单精确度，而double是指双精确度）。

该标准规定了四种表示浮点数值的方式，优点是：可以归一化处理整数和小数。

javascript 对 number 数值的表示方式则采用了其中的双精确度（64位）的表示方式，所以 javascript 中所有的数值都是 number 类型，因为它既可以表示浮点数值，也可以表示整数。

基础知识

在介绍数字的IEEE 754存储之前，先介绍一下下面的几个基础知识：

十进制转为二进制
二进制科学计数法
二进制转为十进制

为什么要介绍上面的知识呢，因为数字在内存中存储的是数字的二进制的科学计数法。

十进制转为二进制方法

下面以 173.8125 举例如何将之转化为二进制小数。

针对整数部分 173，采取除 2 取余，结果逆序排列就将得整数部分的二进制。

173 / 2 = 86 ... 1
86 / 2 = 43 ... 0
43 / 2 = 21 ... 1   ↑
21 / 2 = 10 ... 1   | 逆序排列
10 / 2 = 5 ... 0    |
5 / 2 = 2 ... 1     |
2 / 2 = 1 ... 0
1 / 2 = 0 ... 1

得到整数部分的二进制为 10101101。

针对小数部分 0.8125，采用乘 2 取整，结果顺序排列就得小数部分的二进制。

0.8125 * 2 = 1.625  |
0.625 * 2 = 1.25    | 顺序排列
0.25 * 2 = 0.5      |
0.5 * 2 = 1         ↓

得到小数部分的二进制为 1101

将前面两部的结果相加，结果为 10101101.1101，这就是173.8125这个数的二进制表示。

二进制转为十进制方法

下面以刚刚得到的二进制 10101101.1101 为例进行转换。

针对整数部分 10101101 计算逻辑如下：

// 10101101
// ← 从右往左
1 * 2^0 + 0 * 2^1 + 1 * 2^2 + 1 * 2^3 + 0 * 2^4 + 1 * 2^5 + 0 * 2^6 + 1 * 2^7
= 1 + 0 + 4 + 8 + 0 + 32 + 0 + 128
= 173

小数部分 1101 计算逻辑如下

// 1101
// 从左往右 →
1 * 2^-1 + 1 * 2^-2 + 0 * 2^-3 + 1 * 2^-4
= 1/2 + 1/4 + 0 + 1/16
= 13/16
= 0.8125

最后将整数部分跟小数部分相加得到最终结果 173.8125，和我们刚刚得到的结果一样。

科学计数法

十进制 173.8125 的科学计数法为 1.738125 * 10^2

十进制 173.8125 对应的二进制 10101101.1101，进一步可以使用二进制的科学计数法来表示，对应的二进制科学计数法为 1.01011011101 * 2^7。跟十进制类似，将底数 10 换为了 2，7 则代表小数点往右多少位。

重点 1.01011011101 * 2^7 为二进制，将其转换为 10 进制的过程为，先将 1.01011011101 做为 2 进制转换为 10 进制，得到 1.35791015625，然后将其乘以 2^7 （也就是 1.35791015625 * 128），最后得到的十进制为 173.8125

“浮点数”是一种表示数字的标准，整数也可以用浮点数的格式来存储。我们也可以理解成，浮点数就是小数。在JavaScript中，现在主流的数值类型是Number，而Number采用的是IEEE754规范中64位双精度浮点数编码。这样的存储结构优点是可以归一化处理整数和小数，节省存储空间。

对于一个整数，可以很轻易转化成十进制或者二进制。但是对于一个浮点数来说，因为小数点的存在，小数点的位置不是固定的。解决思路就是使用二进制科学计数法，这样小数点位置就固定了。

`IEEE 754` 规范

前面提到为了归一化处理整数和小数，我们使用二进制科学计数法来表示数。计算机存储的数据是二进制（0或1）表示，先把二进制转换为科学记数法，公式如下：

V = M * 2^E

其中，M的值为[1, 2)的浮点数，且每一位都是0或1，E为小数点移动的位数（肯定为整数），即指数。

举个例子，如：27.0转化成二进制为11011.0

科学计数法表示为：

1.10110 * 2^4

如上M=1.10110，E=4。所以我们需要在内存中存储的数据为1.10110、4这两个数就能通过公式的到二进制表示，进而到十进制表示。因为二进制科学计数法的尾数M的第一位固定的1，所以可以直接省去（这样可以节省一个bit，导致M最多可以表示53位），即最终M=10110。

上面是对于正数而言，如果要区分正负我们需要添加一个符号位来表示，需要占用一个bit，0表示正数，1表示负数。

综上所述，IEEE 754规范中存储二进制的科学计数法分为三个部分：

V = (-1)^S * M * 2^E

这就是IEEE 754规范中存储浮点数的公式，其中S表示符号位，M表示尾数，E表示指数。

下面以双精度（64位）为例

符号位S：第 1 位是正负数符号位（sign），0代表正数，1代表负数。
指数位E：中间的 11 位存储指数（exponent），用来表示次方数，可以为正负数。在双精度浮点数中，指数的固定偏移量为1023。
尾数位M：最后的 52 位是尾数（mantissa），超出的部分自动进一舍零。

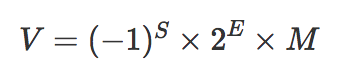
$Number数学计算公式$

三个特殊值`±0`、`±∞`、`NaN`

±0的表示

如果指数是0并且尾数的小数部分是0，这个数±0（和符号位相关）

0 = (-1)^0 * 0 * 2^(0)
-0 = (-1)^1 * 0 * 2^(0)

±∞的表示

如果指数 = 2^11-1并且尾数的小数部分是0，这个数是±∞（同样和符号位相关）

∞ = (-1)^0 * 0 * 2^(2047)
-∞ = (-1)^1 * 0 * 2^(2047)

非数（NaN）

如果指数 = 2^11-1并且尾数的小数部分非0，这个数表示为非数（NaN）

NaN = (-1)^0 * 1 * 2^(2047)

`JavaScript`中`Number`的存储

在JavaScript中Number存储方式是双精度浮点数（64位），其长度为8个字节，即64位比特。

实例分析

下面以27.5为例，存储方式如下：

转换为二进制

将 27.5 转换为二进制11011.1。

转换为二进制科学计数法

11011.1转换为科学记数法表示为-1^0 + 1.10111 * 2^4

根据IEEE 754规则存储。

符号位S为：0(表示正数，任何数的0次幂为1) 指数位E为：5位偏移加上双精度浮点数中指数的固定偏移量1023=1023+4=1027。因为它是十进制的需要转换为二进制，即 10000000011 尾数位M为：这里省略公共整数1为10111，补够52位即： 1011 1000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000

综上所述27.5存储为计算机的二进制标准形式（符号位+指数位+小数部分 (阶数)），如下：

0+10000000011+1011 1000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000

思考 | 疑问

`JavaScript`整数的最大值

JavaScript中Number存储方式是双精度浮点数（64位）能表示的最大整数是2 ^ 53 -1。因为整数需要连续性，所以表示整数时不能使用指数位E区域，只有尾数M区域可表示连续的数据，M一共占用52位，但是如果加上我们省略的首位，其实M最多可以表示53位。所以最大的安全整数是2 ^ 53 -1。大于 9007199254740992 的可能会丢失精度。Number.MAX_SAFE_INTEGER为9007199254740991。

`Array`索引既然是整数,那它的最大索引为什么不是`2 ^ 53 - 1`呢？

JavaScript语言中数组的索引最大就是2^32 -1。就当做语言规范吧，背后的原因不清楚。除了数组索引，还有其他的地方采用32bit整数：

位运算
setTimeout/setInterval的delay参数也是必须是32整数

数组的最大长度是2^32 - 1，这个不是指数组只能存2^32 - 1位数据，也不是说数组的下标最大值就是2^32 - 1，而是指数组的length属性最大值为2^32 - 1。

ECMAScript 标准约定number数字需要被当成 64 位双精度浮点数处理，但事实上，一直使用 64 位去存储任何数字实际是非常低效的，所以 JavaScript 引擎并不总会使用 64 位去存储数字，引擎会在内部采用其他内存表示方式，如 32 位。

`双精度浮点数（64位）`指数位为什么要固定偏移`1023`

首先要明确一点E的值，可能是正数也可能是负数的，对应于右移和左移。

指数部分使用所谓的偏正值形式表示，偏正值为实际的指数大小与一个固定值（64位的情况是1023）的和。采用这种方式表示的目的是简化比较。因为，指数的值可能为正也可能为负，如果采用补码表示的话，全体符号位S和E自身的符号位将导致不能简单的进行大小比较。正因为如此，指数部分通常采用一个无符号的正数值存储。双精度的指数部分是−1022～+1023加上1023，指数值的大小从1～2046（0（2进位全为0）和2047（2进位全为1）是特殊值）。浮点小数计算时，指数值减去偏正值将是实际的指数大小。

浮点数阶码的偏移量就是是为了计算机处理数据的方便，还记得为什么计算机要有补码吗？使用补码原因就是希望在加法运算中将减法运算一并处理了，简化CPU中运算器的设计，确实我们通过补码实现了加减法的统一。现在我们将浮点数用这种形式保存，那么计算机怎么比较浮点数的大小呢？浮点数表示有两个符号位置，一个是数符S，一个是阶码的符号，如果仅仅采用补码作为阶码，由于阶码有正有负，整个数的符号位和阶数的符号位将导致不能进行简单的大小比较，所以阶数采用了一个无符号的正整数存储。阶数的值直接进行二进制计算，符号位置是默认为0的，于是阶数的值可以为0 到 255

指数部分使用了偏正值形式表示后，浮点数基本上可以按照符号位、指数域、尾数域的顺序作字典比较。显然，所有正数大于负数。正负号相同时，指数的二进制表示法更大的其浮点数值更大。

为什么二进制科学计数表示`M`会是`[1, 2)`的浮点数

下面还是以27.0为例来说明：

之前说过27.0的二进制科学计数法表示为：

1.10110 * 2^4

其实还可以表示其他格式的，如下：

0.110110 * 2^5

这种方式虽然数学上也是一样的，但是占用的存储会不一样，比如存储110110比存储10110多用一位，5也比4大，这样就导致同样大小的内存，存放的数据不一样。其实就是我们默认省略的1是一个有效信息，比省略一个首位的0，多了一个有效信息，所以M的值选择移位到[1, 2)的浮点数，其首位为必然是1。

提示我们选择二进制的指数表示时，将M表示为1.****是因为任何数都可以表示成这个格式。如果所以得值有更大的公共前缀，当然会选择这个最大的公共前缀来当整数，这样就能省略掉了。

举个例子，如果仅考虑110001和110010这两个二进制数，那我们肯定会选择下面的存储方式：

110001 => 11.0001 * 2^4
M=0001
E=4

110010 => 11.0010 * 2^4
M=0010
E=4

这样表示后，解析的时候，直接加上整数位11即可。

指数位`E`为什么是`11`位，尾数位`M`才52位，偏移量用不了`11`啊

单精确度（32位）中有8位指数位，23位尾数位 双精确度（64位）中有11位指数位，52位尾数位

感觉这些尾数位，做偏移用不了这么指数位的。我能想到的是为了后面的扩展而设计的，之前还去知乎提过问，IEEE754，float、double指数位为什么是8位、11位？。大家有什么想法欢迎交流。

`0.1 + 0.2 不等于 0.3`的原因

JS和toFixed也能看到实际的值。toFixed() 方法可把 Number 四舍五入为指定小数位数的数字。

Number.MAX_SAFE_INTEGER.toFixed(64)
"9007199254740991.0000000000000000000000000000000000000000000000000000000000000000"
Number.MAX_SAFE_INTEGER
9007199254740991
(0.1).toFixed(64)
"0.1000000000000000055511151231257827021181583404541015625000000000"
(0.2).toFixed(64)
"0.2000000000000000111022302462515654042363166809082031250000000000"
(0.1 + 0.2).toFixed(64)
"0.3000000000000000444089209850062616169452667236328125000000000000"
0.1 + 0.2 == 0.3
false

0.1 + 0.2 不等于 0.3原因很简单，因为0.1存储的值比实际值大了一点，0.2也是大了一点（差值比0.1大一倍），两个相加就大很多了，多出来的就是那个尾巴，当偏移大于最小精度时就会出现误差。说到得的原因还是二进制计数不能精确的表示一些小数导致的。

`二进制计数`不能精确的表示一些小数

二进制计算能精确表示的小数肯定是能够通过不断乘以2的到结果为1的数的和，比如0.5、0.25、0.125等。不能精确表示0.1之类的数。

为什么0.1不能够被准确存储呢？因为计算机都是二进制的，在十进制能表示的数不一定能被二进制精确表示，就好像在十进制里面无法准确表示1/3一样，而在三进制里面0.1便表示1/3了。在二进制里面能够被精确表示都必须得是二的倍数的组合，如二进制的0.1表示十进制的0.5，0.11便表示0.75（0.5 + 0.25），0.111表示0.875（0.5 + 0.25 + 0.125），假设现在要存储0.625那么能够被精确表示为二进制的0.101，如果要表示0.626呢？那么应该是通过后面的小数位相加拼凑，让其尽可能逼近0.626. 这个时候就不是精确表示了，这个事情就是编译器的工作。

提示这里所说的最小表示精度，是有尾数位M的大小决定的

`JavaScript`大数问题解决

下面等式成立

Number.MAX_SAFE_INTEGER + 1 === Number.MAX_SAFE_INTEGER + 2

超出了最大安全范围

(Number.MAX_SAFE_INTEGER + 1).toFixed(64)
"9007199254740992.0000000000000000000000000000000000000000000000000000000000000000"
(Number.MAX_SAFE_INTEGER + 2).toFixed(64)
"9007199254740992.0000000000000000000000000000000000000000000000000000000000000000"
(Number.MAX_SAFE_INTEGER + 3).toFixed(64)
"9007199254740994.0000000000000000000000000000000000000000000000000000000000000000"
(Number.MAX_SAFE_INTEGER + 4).toFixed(64)
"9007199254740996.0000000000000000000000000000000000000000000000000000000000000000"
(Number.MAX_SAFE_INTEGER + 5).toFixed(64)
"9007199254740996.0000000000000000000000000000000000000000000000000000000000000000"
(Number.MAX_SAFE_INTEGER + 6).toFixed(64)
"9007199254740996.0000000000000000000000000000000000000000000000000000000000000000"
(Number.MAX_SAFE_INTEGER + 7).toFixed(64)
"9007199254740998.0000000000000000000000000000000000000000000000000000000000000000"

为了处理超过整数最大安全范围的数字，需要考虑其他方案。

decimal.js 字符串的形式计算，以性能换精度。
BigInt 新类型，字符串n结尾，如：9007199254740993n

参考

IEEE 754

IEEE 754 Converter （在线查看）

IEEE754，float、double指数位为什么是8位、11位？

JS Number精度

计算机编程语言中里有提到浮点类型float和double采用了IEEE754格式有参考价值

版权所有

版权归属：唐道勇

本文链接：/article/38rd8vft.html